FIT5124 Assignment 1 - Encrypted Database Attacks & Countermeasures

Posted on Edited on In ,
This report is related to FIT5124 2021S1 Assignment 1. The main aspects that this assignment reviews are 2 types of encrypted database: SSE & PPE. We will introduce the main attacks & main countermeasures about them.


Assignment Requirements

You can find it in: https://github.com/RdWeirdo981/Master-of-Cybersecurity/blob/main/2021S1%20FIT5124%20Advanced%20Security%20Topics/A1/FIT5124-S1-2021-A1.pdf

Task 1: Reading Encryption Scheme

Security Definition

Security Analysis

Task 2: Count Attacks against Searchable Symmetric Encryption

Case study I

d1 = {w1, w2, w3, w4, w6} d2 = {w1, w2, w3, w6}

d3 = {w1, w2, w4, w6} d4 = {w1, w4, w6}

d5 = {w4, w5, w6} d6 = {w4, w6}

We can convert this into a table:

d1 d2 d3 d4 d5 d6
w1 1 1 1 1
w2 1 1 1
w3 1 1
w4 1 1 1 1 1
w5 1
w6 1 1 1 1 1 1

We then generate the keyword co-occurrence matrix (presented as the table below):

w1 w2 w3 w4 w5 w6
w1 4
w2 3
w3 2
w4 5
w5 1
w6 6

In general, we have to fill the rest of the table. But in this case, since the numbers in diagonal are all unique, we can simply deduct the match between keywords and queries without the grey numbers. (I put them here for better understanding how key-word co-occurrence works.)

  1. q1 matches 5 permuted document IDs, and w4 matches 5 document IDs too. Thus, q1 = w4.

  2. q2 matches 2 permuted document IDs, and w3 matches 2 document IDs too. Thus, q2 = w3.

  3. q3 matches 4 permuted document IDs, and w1 matches 4 document IDs too. Thus, q3 = w1.

  4. q4 matches 3 permuted document IDs, and w2 matches 3 document IDs too. Thus, q4 = w2.

  5. q5 matches 6 permuted document IDs, and w6 matches 6 document IDs too. Thus, q5 = w6.

  6. q6 matches 1 permuted document IDs, and w5 matches 1 document IDs too. Thus, q6 = w5.

Case study II

d1 = {w1, w2, w3, w4, w6} d2 = {w2, w3, w6}

d3 = {w1, w3, w4, w6} d4 = {w1, w4, w6}

d5 = {w4, w5, w6} d6 = {w5}

d1 d2 d3 d4 d5 d6
w1 1 1 1
w2 1 1
w3 1 1 1
w4 1 1 1 1
w5 1 1
w6 1 1 1 1 1
w1 w2 w3 w4 w5 w6
w1 3 1 2 3 0 3
w2 1 2 2 1 0 2
w3 2 2 3 2 0 3
w4 3 1 2 4 1 4
w5 0 0 0 1 2 1
w6 3 2 3 4 1 5
q eids Total number
q1 e2 e3 e4 e5 e6 5
q2 e2 e3 e5 e6 4
q3 e1 e3 2
q4 e4 e5 2
q5 e2 e5 e6 3
q6 e4 e5 e6 3

Analysis:

  1. Unique pair:

q1 = w6, for unique occurrence 5.

q2 = w4, for unique occurrence 4.

  1. Possible pairs:

{q3, q4} × {w2, w5} for occurrence 2.

{q5, q6} × {w1, w3} for occurrence 3.

  1. We will need query co-occurrence matrix.
q1 q2 q3 q4 q5 q6
q1 5 4 1 2 3 3
q2 4 4 1 1 3 2
q3 1 1 2 0 0 0
q4 2 1 0 2 1 2
q5 3 3 0 1 3 2
q6 3 4 0 2 2 3

Usually, we will observe the unique correlation of q3-q6 with q1 & q2, but here we have a special pattern: correlation 0 only occurs in q3 & w5. Thus, we immediately know that q3 = w5, which leads to the other pair q4 = w2.

Check:

Correlation(w2, w4) = 1 = Correlation(q4, q2)

Correlation(w2, w6) = 2 = Correlation(q4, q1)

Thus, this is correct.

Finally, we will look at {q5, q6} × {w1, w3}.

By observing, we should use q6 as our break point.

Correlation (q6, q2) = 2 = Correlation (w3, w4), and this is a unique correlation. Thus, q6 = w3, which also leads to q5 = w1.

Check:

Correlation (q5, q1) = 3 = Correlation (w1, w6)

Correlation (q5, q2) = 3 = Correlation (w1, w4)

Thus, this is correct.

  1. The counterattack does recover all queries, and the final results are below:

q1 = w6 q2 = w4 q3 = w5

q4 = w2 q5 = w1 q6 = w3

Case study III

d1 = {w1, w2, w3, w6} d2 = {w2, w3, w4, w6} # update!

d3 = {w1, w2, w3, w4, w6} d4 = {w1, w3, w4, w6}

d5 = {w5, w6} d6 = {w5, w6}

d1 d2 d3 d4 d5 d6
w1 1 1 1
w2 1 1 1
w3 1 1 1 1
w4 1 1 1
w5 1 1
w6 1 1 1 1 1 1
w1 w2 w3 w4 w5 w6
w1 3 2 3 2 0 3
w2 2 3 3 1 0 3
w3 3 3 4 2 0 4
w4 2 1 2 3 0 2
w5 0 0 0 0 2 2
w6 3 3 4 2 2 6
q eids Total number
q1 e1 e5 e6 3
q2 e1 e2 e6 3
q3 e3 e4 2
q4 e1 e2 e3 e4 e5 e6 6
q5 e2 e5 e6 3
q6 e1 e2 e5 e6 4
q1 q2 q3 q4 q5 q6
q1 3 2 0 3 2 3
q2 2 3 0 3 2 3
q3 0 0 2 2 0 0
q4 3 3 2 6 3 4
q5 2 2 0 3 3 3
q6 3 3 0 4 3 4

Analysis:

  1. We notice that the occurrence in query does not totally match occurrence in keyword. This is an obvious evidence that the encryption has some padding.(Since the assignment has been updated, this is not the situation.)

So, I’d like to start from Correlation 0, since the padding can only add files rather than removing files. Thus, we can see the only one who has Correlation = 0 more than once is q3 & w5.

q3 = w5

  1. Unique pair

But we are lucky. Since the unique occurrence 4 and 6 in keyword matrix are larger than other occurrences, and in query matrix they are also unique and larger than others, we can conclude that they are matched.

Thus, q4 = w6, and q6 = w3.

  1. Possible pair

{q1, q2, q5} × {w1, w2, w4}

We will analyze the Correlation between them and the revealed pairs.

For w3:

Correlation (w3, w1) = 3 Correlation (q6, q1) = 3

Correlation (w3, w2) = 3 & Correlation (q6, q2) = 3

Correlation (w3, w4) = 2 3 Correlation (q6, q5) = 3

This tells nothing.

For w5:

Correlation (w5, w1) = 0 Correlation (q3, q1) = 0

Correlation (w5, w2) = 0 & Correlation (q3, q2) = 0

Correlation (w5, w4) = 0 Correlation (q3, q5) = 0

This gives no information.

For w6, situations are similar.

It seems that we have no way to go. But hang on, can we break this by matching eid & id?

q3 = w5: {e3, e4} × {d5, d6}, thus {e1, e2, e5, e6} × {d1, d2, d3, d4}

We can observe this:

q1 e1 e5 e6
q2 e1 e2 e6
q5 e2 e5 e6
d1 d2 d3 d4
w1 1 1 1
w2 1 1 1
w4 1 1 1

Thus, e6 = d3. And you can finally conclude that no more information can be retrieved further. Sorry, adversary!

  1. Information that leaks:

q3 = w5 q4 = w6 q6 = w3

e6 = d3

possible pairs: {q1, q2, q5} × {w1, w2, w4}

possible eid & id matches: {e3, e4} × {d5, d6}, {e1, e2, e5} × {d1, d2, d4}

Task 3: Padding Countermeasures in Searchable Symmetric Encryption

I wrote 3 .py files to not only calculate the result, but also finish the padding and output as .txt files. I will only put the main part of my code here, so you won’t see something like writer.write repeatedly.

Approach #1

Source code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
longest = 0
for id_list in inverted_dict.values():
    if len(id_list) > longest:
        longest = len(id_list)
    
# append pid & count real & padding
count_real = 0
count_padding = 0
for id_list in inverted_dict.values():
    count_real += len(id_list)
    if len(id_list) < longest:
        diff = longest - len(id_list)
        for i in range(diff):
            # id_list.add(utilities.generate_random_id())
            # because the program runs so slow, we replace the generator with i. But in real case, we will use generate_random_id().
            id_list.add(i)
            count_padding += 1
            print("added!",count_padding)

# calculate overhead
pad_overhead = (count_real + count_padding) / count_real

print("Approach 1")
print("The count of padding is: " + str(count_padding))
print("The count of real pairs is: " + str(count_real))
print("The padding overhead is: " + str(pad_overhead))

The padding solution is to pad the id list of each keyword whose length(i.e., frequency; i.e., number of file id) is not the longest length to the longest length.

Results:

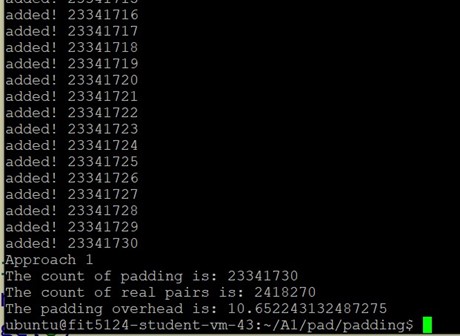
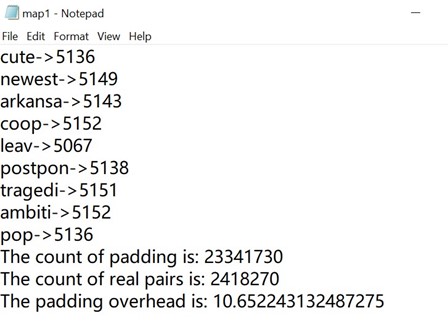
The overhead is ~10.65.

Approach #2

Source code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# select multiplication
n = 100
# append pid to the nearest multiplication of 5 & count padding
count_real = 0
count_padding = 0
for id_list in inverted_dict.values():
    count_real += len(id_list)
    i = 1
    while (len(id_list) > i * n):
        i += 1 # find the nearest 5i larger than len(id_list)
    if len(id_list) < i*n:
        diff = i*n - len(id_list)
        for i in range(diff):
            if i in id_list:
                id_list.add(utilities.generate_random_id)
            else:
                id_list.add(i)
            count_padding += 1
            print("added!",count_padding)
# calculate overhead
pad_overhead = (count_real + count_padding) / count_real

The padding solution is to pad the id list of each keyword whose length is not a multiplication of 100 to the nearest multiplication of 100 larger than the original length.

Results:

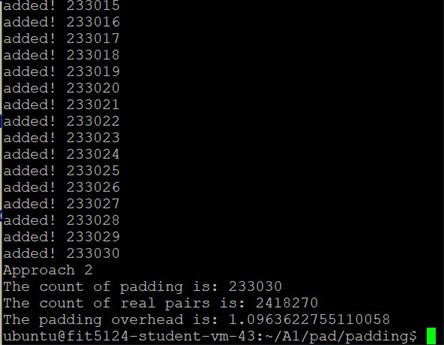
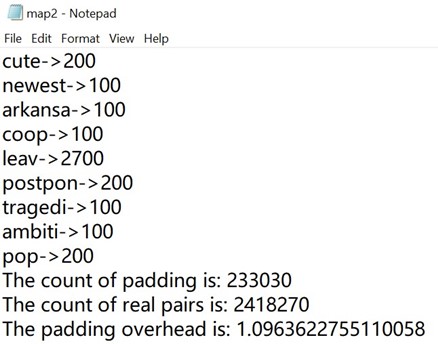
The overhead is ~1.10.

Approach #3

Source code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
file = open(frequency_file, "r", newline='')
csv_reader = csv.reader(file,delimiter=',')
for i, row in enumerate(csv_reader): #i starts from 0
    id_list.append(int(row[1]))
#cluster size: 256, 512
cluster_points_256 = [0,392,648,904,1160,1416,1672,1928,2184,2440,2696,2952,3208,3464,3720,3976,4232,4488,4744,5000]
cluster_points_512 = [0,904,1416,1928,2440,2952,3464,3976,4488,5000]

# cluster padding
def app_3 (cluster_points,number):
    count_padding = 0
    count_real = 0
    for id_set in inverted_dict.values():
        count_real += len(id_set)
        for i in range(len(cluster_points)-1):
            highest = id_list[cluster_points[i]]
            lowest = id_list[cluster_points[i+1]-1]
            if len(id_set) >= lowest and len(id_set) <= highest:
                diff = highest - len(id_set)
                if diff != 0:
                    for k in range(diff):
                        id_set.add(k)
                        count_padding += 1
                        print("added!",count_padding)
    # calculate overhead
    pad_overhead = (count_real + count_padding) / count_real
    print("Approach 3", number)
    print("The count of padding is: " + str(count_padding))
    print("The count of real pairs is: " + str(count_real))
    print("The padding overhead is: " + str(pad_overhead))

#app_3(cluster_points_256, 256)
app_3(cluster_points_512, 512)

This padding solution is to use a cluster to put the keywords having similar frequencies into one small group and inside the group, pad all keywords to the largest frequency.

Results:

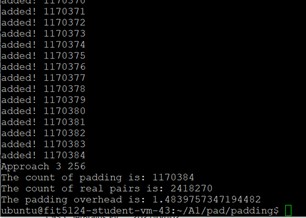
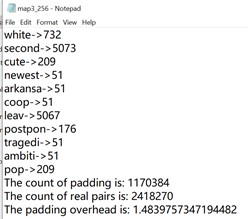
App #3 – 256

App #3 – 512

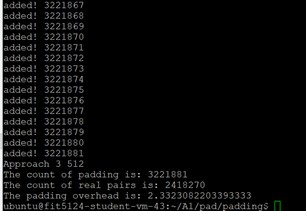
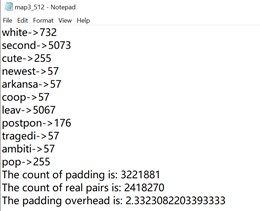
The overhead for cluster 256 is ~1.48, for cluster 512 is ~ 2.33.

Comparison

Approach #1 Approach #2 Approach #3 – 256 Approach #3 – 512
Padding overhead ~10.65224 ~1.09636 ~1.48398 ~2.33231

The biggest overhead is approach #1, which is also called native padding.

App #2 has the smallest padding overhead, but we can see from the Fig 5.2.2: it’s very easy to guess that the padding pattern is multiplication of 100. Although we are not required to calculate the recovery ratio, we can observe the security strength of App #2 should be weaker than App #3.

Thus, under the same comparable security strength, the minimal padding will be App #3. We can also see that cluster 256 is smaller than cluster 512. This is because the smaller the cluster group is, the less padding will the approach need.

Task 4: Inference Attacks against Order-preserving Encryption

Source code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import random
import os
import operator
import csv
from itertools import cycle
import numpy as np
from scipy.optimize import linear_sum_assignment

def cumulative_attack(raw_data,ope_data):

    #Step 1: compute the histograms of list_raw_data and ope_data
    raw_data_hist = {}
    ope_data_hist = {}
    histo(raw_data, raw_data_hist)
    histo(ope_data, ope_data_hist)
    
    #Step 2: compute emperical CDFs of raw and ope data
    raw_data_keys = sorted(list(raw_data_hist.keys()))
    ope_data_keys = sorted(list(ope_data_hist.keys()))
    
    raw_data_cdf = cdf_histo(raw_data_keys, raw_data_hist)
    ope_data_cdf = cdf_histo(ope_data_keys, ope_data_hist)
      
    #Step 3_1: Compute the cost matrix C and then use LSAP
    C =   [[] for _ in range(len(ope_data_keys))]
    
    for i in range(len(ope_data_keys)):
        for j in range(len(raw_data_keys)):
            C[i].append((abs(ope_data_hist[ope_data_keys[i]] - raw_data_hist[raw_data_keys[j]]))**2 + (abs(ope_data_cdf[ope_data_keys[i]] - raw_data_cdf[raw_data_keys[j]]))**2)

    #Step 3_2: apply linear_sum_assignment to identify the weight matrix X
    row_ind, col_ind = linear_sum_assignment(C) 
    
    	#Step 4: export the mapping
    with open("map.txt", "w", newline='') as writer:
        writer.write("enc_age,raw_age\n")  
        for index in range(len(raw_data_keys)):
            writer.write(str(ope_data_keys[index]) + "->" + str(raw_data_keys[col_ind[index]])+ "\n")
    writer.close() 
    return 0

def file_reader (reader, lst,index):

    for i, row in enumerate(reader): #i starts from 0
        if i!=0:
            lst.append(int(row[index]))
            
def histo (list_data, dic):
    
    for item in list_data: #i starts from 0
        if item in dic:
            dic[item] += 1
        else:
            dic[item] =1

def cdf_histo (sorted_list_data, dic):
    
    new_dic = dic.copy()

    for index in range(len(sorted_list_data)):
        if index != 0:
            new_dic[sorted_list_data[index]] += new_dic[sorted_list_data[index-1]]
    return new_dic
  
if __name__ == '__main__':
    #raw dict and enc dict
    raw_age= list()
    enc_age = list()
    #read the plaintext  file
    plaintext_file = open("auxiliary.csv", "r", newline='') #   covid_true dataset.csv
    p_reader = csv.reader(plaintext_file,delimiter=',')
    file_reader(p_reader,raw_age,0)
    #read the cipher  file
    cipher_file = open("ope_enc_covid_age.csv", "r", newline='')
    c_reader = csv.reader(cipher_file,delimiter=',')
    file_reader(c_reader,enc_age,0)
    cumulative_attack(raw_age,enc_age)

Results:

enc_age,raw_age

0->0

1->1

11->2

18->3

22->4

39->5

46->6

52->7

56->8

62->9

63->10

69->11

73->12

77->13

79->14

93->15

95->16

100->17

102->18

104->19

107->20

117->21

120->22

141->23

149->24

150->25

153->26

159->27

162->28

163->29

168->30

172->31

186->32

191->33

193->34

206->35

207->36

208->37

209->38

211->39

212->40

217->41

226->42

230->43

232->44

238->45

255->46

259->47

263->48

264->49

270->50

271->51

275->52

276->53

277->54

278->55

284->56

286->57

293->58

295->59

297->60

300->61

310->62

313->63

315->64

317->65

327->66

332->67

337->68

339->69

345->70

353->71

356->72

357->73

359->74

365->75

369->76

378->77

383->78

387->79

394->80

402->81

407->82

409->83

410->84

414->85

424->86

428->87

430->88

431->89

432->90

434->91

438->92

447->93

459->94

466->95

468->96

To check this result, I sorted the 2 .csv files in ascending order in Excel and observe the matches. It’s evident that this result is correct.